Bayesian Inference about Outputs of Computationally Expensive Algorithms with Uncertainty on the Inputs
Figure 8: Graphical model for Bayesian emulator
Bayesian inference allows us to treat unknown variables as random variables, even if the computer code is deterministic, i.e. the results do not change between two identical runs.
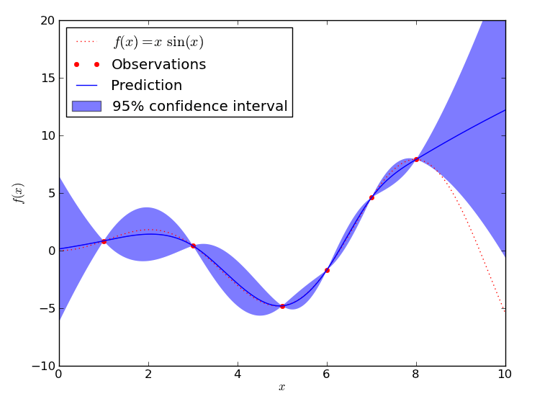
Typically, Gaussian processes with specified means and variance functions are used to model computer simulations. This framework will be adopted in this project. The objective of this project is primarily to understand Gaussian processes and formulate a methodology for developing Gaussian process emulators for nuclear reactor simulation codes that compute the nuclear power and temperature distribution in 3D mesh space as well as their variation in time.
We have investigated sensitivity of reactivity insertion transient to the uncertainties in the input parameters. The effect of uncertainties of the identified input parameters has been studied, including the effective conductivity of the three layers in the fuel pebble, the specific heat capacity of the three layers in the fuel pebble and of the coolant, and etc. Uncertainty propagation of more complex 2D and 3D models will be studied.